الضرب الداخلي على المصفوفات والاقترانات المتصلة (Inner Product)

الضرب الداخلي (Inner Product)على المتجهات و كثيرات الحدود والمصفوفات والاقترانات المتصلة

في هذه المحاضرة سنتعرف على

تعريف الضرب القياسي - Dot Product
تعريف الضرب الداخلي - Inner Product
الضرب الداخلي على المتجهات - Inner product on vectors
الضرب الداخلي على المصفوفات - Inner product on matrix
الضرب الداخلى على كثيرات الحدود - Inner product on polynomials
الضرب الداخلي على الاقترانات المتصلة - inner product on continious functions

الضرب الداخلي (Inner Product) هو تعميم لعملية الضرب القياسي او النقطي (Dot Product) حيث ان الضرب القياسي يكون معرفا على عملية الضرب القياسية Standard Operation of Product ويسمى (Eclidean Inner Product)

تعريف الضرب القياسي لمتجيهين (Dot Product) وإيجاد طول المتجه (Norm)والمسافة بين المتجهين (Distance)

$https://latex.codecogs.com/svg.image?let u,v\in R^{n}, \ \ \ \textbf{u}=(u_1,u_2,...,u_{n})\ \ \textbf{v}=(v_1,v_2,...,v_{n})$

فان الضرب القياسي يعرف كما يلي

$https://latex.codecogs.com/svg.image? u.v=(u_1,u_2,...,u_{n}).(v_1,v_2,...,v_{n})=u_1v_1+u_2v_2+....+u_nv_n$

اي يتم ضرب كل مركبة من المتجه الاول في المركبة المناظرة لها في المتجه الثاني , " عملية الضرب القياسية لمتجهين"

مثال : اوجد حاصل الضرب القياسي للمتجهين المعرفين كما يلي ثم اوجد طول المتجه u والمسافة بين المتجهين

$https://latex.codecogs.com/svg.image? u,v\in R^2,\ \ u=(2,4),\ v=(-1,-3)\\Dot product \ \ \ u.v=(2)(-1)+(4)(-3)=-2+(-12)=-14\\Norm \ \ u \ \ \ \left\|u \right\| =\sqrt{u.u}=\sqrt{(2)(2)+(4)(4)}=\sqrt{4+16}=\sqrt{20}\\u-v=(2,4)-(-1,-3)=(3,7)\\Distance \ \ \ d(u,v)=\left\| u-v\right\|= \sqrt{(3)(3)+(7)(7)}=\sqrt{58}$

ملاحظة : عند ايجاد الضرب القياسي لمتجهين فان عملية الضرب لا تتغير ( عملية الضرب القياسية الموضحة في التعريف والمثال )

تعريف الضرب الداخلي (Inner Product) وإيجاد طول المتجه (Norm)والمسافة بين المتجهين (Distance)

لاحظنا ان الضرب القياسي (Dot product) يكون معرف على عملية الضرب القياسية بين متجهين بينما في الحالة العامة وهي حالة الضرب الداخلي (Inner Product) من الممكن ان نقوم بتعريف اخر لعملية الضرب بشرط ان تكون هذه العملية تحقق 4 بديهيات وهي

$https://latex.codecogs.com/svg.image?\bullet\left<u,v \right> =\left<v, u\right>\\\bullet \left<u+v,w \right>=\left<u,w \right>+\left<v,w \right>\\\bullet k\left< u,v\right>=\left<ku,v \right>\\\bullet \left<v,v \right>\geq 0\Leftrightarrow v\geq 0$

البديهية الاولى هي بديهية التبديل ، والثانية هي بديهية الجمع ، والثالثة بديهية التماثل والبديهية الاخير بديهية الايجابية

مثال : بين ان التعريف التالي هو ضرب داخلي (Inner Product)

$https://latex.codecogs.com/svg.image?u,v\in R^2 \ \ \left< u,v\right>=3u_1v_1+2u_2v_2$

السؤال بمعنى اخر هل تتحقق البديهيات الأربعة حتى يكون فعلا هذا التعريف هو ضرب داخلي ؟

البديهية الأولى لتحقيقها تحتاج ان تعرف ان مركبات المتجه هي اعداد حقيقية وبالتالي تتحقق خاصية التبديل

$https://latex.codecogs.com/svg.image?\left<u,v \right>=3u_1v_1+2u_2v_2\\ \ \ = 3v_1u_1+2v_2u_2=\left<v,u \right>$

البديهية الثانية نستخدم التعريف ثم عملية تبديل وتجميع للحدود فنجد انها أيضا تتحقق

$https://latex.codecogs.com/svg.image?\left<u+v,w \right>=3(u_1+v_1)w_1+2(u_2+v_2)w_2\\ \ \ = 3u_1w_1+3v_1w_1+2u_2w_2+2v_2w_2 \\=(3u_1w_1+2u_2w_2 )+(3v_1w_1+2v_2w_2 )\\=\left<u,w \right>+\left<v,w \right>$

البديهية الثالثة استخدم التعريف وعملية الضرب نجد انها تتحقق

$https://latex.codecogs.com/svg.image?k\left<u,v \right>=k(3u_1v_1+2u_2v_2)\\ =3ku_1v_1+2ku_2v_2\\ =3\left ( ku_1 \right )v_1+2\left ( ku_2 \right )v_2\\ =\left<ku,v \right>$

البديهية الرابعة استخدم التعريف وخواص العدد المربع نجد انها تتحقق

$https://latex.codecogs.com/svg.image?\left<v,v \right>=3v_1v_1+2v_2v_2\\ =3v_{1}^{2}+2v_{2}^{2}\geqslant 0$

بما ان جميع البديهيات تتحقق اذن التعريف هو ضرب داخلي (Inner Product)

مثال : الضرب الداخلي على المتجهات Inner Product on vectors اوجد ما يلي

$https://latex.codecogs.com/svg.image?\left<\ \,,\ \right>,\ \ \left\|\ \right\|, d(\ \,\ \)$

$https://latex.codecogs.com/svg.image?. u,v\in R^2,\ \ u=(1,0),\ v=(0,1)\ \ \ \ \ \left<u,v \right>=3u_1v_1+2u_2v_2\\Inner \ \ product \ \ \ \left<u,v \right>=3(1)(0)+(0)(1)=0 \\Norm \ \ u \ \ \ \left\|u \right\| =\sqrt{\left<u,u \right>}=\sqrt{3(1)(1)+2(0)(0)}=\sqrt{3+0}=\sqrt{3}\\ u-v=(1,0)-(0,1)=(1,-1)\\Distance \ \ \ d(u,v)=\left\| u-v\right\|= \sqrt{3(1)(1)+2(-1)(-1)}=\sqrt{5 }$

مثال : الضرب الداخلي على كثيرات الحدود Inner Product on Pn اوجد ما يلي

$https://latex.codecogs.com/svg.image?\left<\ \,,\ \right>,\ \ \left\|\ \right\|, d(\ \,\ \)$

$https://latex.codecogs.com/svg.image?. p,q\in P(x),\ \ p(x)=-2+x,\ q(x)=4-7x\ \ \ \ \ \left<p,q \right>=3p_1q_1+2p_2q_2\\Inner \ \ product \ \ \ \left<p,q \right>=3(-2)(4)+2(1)(-7)=-38 \\Norm \ \ p \ \ \ \left\|p \right\| =\sqrt{\left<p,p \right>}=\sqrt{3(-2)(-2)+2(1)(1)}=\sqrt{12+2}=\sqrt{14}\\ p-q=-2+x-(4-7x)=-6+8x\\Distance \ \ \ d(p,q)=\left\| p-q\right\|= \sqrt{3(-6)(-6)+2(8)(8)}=\sqrt{236 }$

مثال : الضرب الداخلي على المصفوفات Inner Product on matrix اوجد ما يلي

$https://latex.codecogs.com/svg.image?\left<\ \,,\ \right>,\ \ \left\|\ \right\|, d(\ \,\ \)$

$https://latex.codecogs.com/svg.image?A,B\in M_2\times 2, \ \ A=\begin{pmatrix}3 & -2 \\ 4& 8 \\\end{pmatrix}, \ \ \begin{pmatrix}-1 & 3 \\ 1& 1 \\\end{pmatrix}\\\left< A,B\right> =a_1b_1+a_2b_2+a_3b_3+a_4b_4, \ \ \ \$

الحل:

$https://latex.codecogs.com/svg.image?Inner \ product \ \ \ \left< A,B\right>=(3)(-1)+(-2)(3)+(4)(1)+(8)(1)=3$ $https://latex.codecogs.com/svg.image?Norm \ \ A= \left\|A \right\|=\sqrt{\left<A,A \right>}=\sqrt{3^{2}+2^2+4^2+8^2}=\sqrt{93}$ $https://latex.codecogs.com/svg.image?A-B=\begin{pmatrix}4 & -5 \\3 & 7 \\\end{pmatrix}\\Distance \ \ =\left\| A-B\right\| =\sqrt{\left<A-B,A-B \right>}=\sqrt{4^2+(-5)^2+3^2+7^2}=\sqrt{99}$

مثال : الضرب الداخلي على الاقترانات المتصلة على فترة [a,b] Inner Product on C اوجد ما يلي

$https://latex.codecogs.com/svg.image?\left<\ \,,\ \right>,\ \ \left\|\ \right\|, d(\ \,\ \)$

$https://latex.codecogs.com/svg.image?f,g\in C[0,1] , \ \ f(x)=x, \ \ g(x)=e^x\\\left<f,g \right> =\int_{0}^{1}f(x)g(x)dx$

الحل:

$https://latex.codecogs.com/svg.image?Inner \ product \ \ \left< f,g\right>=\int_{0}^{1}xe^xdx=[xe^x-e^x]_{0}^{1}=1$ $https://latex.codecogs.com/svg.image?Norm \ f \ \ =\sqrt{\left< f,f\right>}=\sqrt{\int_{0}^{1}x^2dx}=[\frac{x^3}{3}]_{0}^{1}=\frac{1}{3}$

منصة العلوم الرياضية

القائمة الرئيسية

الصفحات

الضرب الداخلي على المصفوفات والاقترانات المتصلة (Inner Product)

الضرب الداخلي (Inner Product)على المتجهات و كثيرات الحدود والمصفوفات والاقترانات المتصلة

تعريف الضرب القياسي لمتجيهين (Dot Product) وإيجاد طول المتجه (Norm)والمسافة بين المتجهين (Distance)

تعريف الضرب الداخلي (Inner Product) وإيجاد طول المتجه (Norm)والمسافة بين المتجهين (Distance)

أخر المواضيع من قسم : جبر خطي

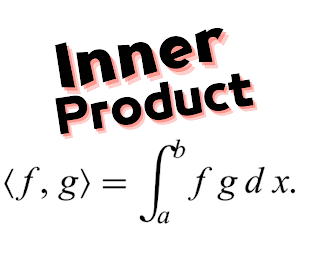
تعليقات

إرسال تعليق