ملزمة الاوائل في الفيزياء للصف 12 العلمي للعام 2023-2024

 أسئلة امتحانات سابقة للتحقق من الان الاقتران حلا للمعادلة التفاضلية 

السؤال الاول : اثبت ان الاقتران

حلا للمعادلة التفاضلية 

تصنيف المعادلة التفاضلية :
الرتبة الثانية والدرجة الأولى وخطية 
الاقتران من الرتبة الثانية وبالتالي نريد إيجاد المشتقة الأولى والمشتقة الثانية ثم التعويض بالاقتران لإثبات ان هذا الاقتران حلا للمعادلة التفاضلية 
المشتقة الأولى : 

مشتقة الاقتران الاسي = مشتقة الاس مضروبا في الاقتران الاسي نفسه 
مشتقة الثابت يساوي صفر 

المشتقة الثانية : نجد المشتقة الثانية بنفس طريقة الاشتقاق 

بالتعويض في المعادلة التفاضلية عن قيمة المشتقات الناتجة نجد ان 

أي ان الطرف الايسر للمعادلة يساوي الطرف الأيمن وبالتالي فان الاقتران المعطى يحقق المعادلة وبالتالي هو حلا لها 

السؤال الثاني : اذا كان لديك الاقتران التالي  

اثبت ان الاقتران يحقق المعادلة التفاضلية التالية وبالتالي حلا لها 

تصنيف المعادلة التفاضلية : الرتبة الاولى والدرجة الاولى وخطية 
بما ان رتبة المعادلة هي الرتبة الاولى اذن نريد ايجاد المشتقة الاولى للاقتران ثم التعويض في المعادلة التفاضلية 
المشتقة الاولى : 

مشتقة الثابت c =صفر ، مشتقة x بالنسبة ل y يساوي 1 ، مشتقة x^2 بالنسبة ل y يساوي = 2x

الان بالتعويض عن قيمة المشتقة في المعادلة التفاضلية نجد ان الطرف الايمن للمعادلة = الطرف الايسر 

وبالتالي فان الاقتران يحقق المعادلة وهو حلا لها 

السؤال الثالث : تحقق من ان الاقتران 

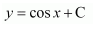
حلا للمعادلة التفاضلية الخطية التالية 

المعادلة التفاضلية من الرتبة الاولى لذلك لتحقيقها بواسطة الاقتران يجب ان نجد المشتقة الاولى والتعويض عنها في الاقتران 
المشتقة الاولى : 

مشتقة الاقتران المثلثي cosx يساوي sinx- ، ومشتقة الثابت يساوي 0

بالتعويض عن قيمة مشتقة الاقتران في المعادلة نجد ان الطرف الايمن = الطرف الايسر للمعادلة وبالتالى فان الاقتران يحقق المعادلة 

                         0=
اذن الاقتران حلا للمعادلة التفاضلية

السؤال الرابع : لديك الاقتران التالي 

استخدم التعويض لإثبات ان الاقتران حلال للمعادلة التفاضلية التالية 

المعادلة التفاضلية هي معادلة خطية من الرتبة الأولى 
المشتقة الاولى :

يمكن استخدام العلاقة التالية لايجاد المشتقة حيث ان مشتقة اقتران جذري = 1/2f(x) مضروب في مشتقة f(x)

مشتقة ال1 =0 ومشتقة x^2 تساوي 2x 

بالتعويض عن قيمة y (الاقتران المعطى)

بالاختصار البسط مع المقام 

بضرب كلا من البسط والمقام في العدد 2 

الطرف الايسر يساوي الطرف الايمن وبالتالي الاقتران يحقق المعادلة وهو حلا لها 

السؤال الخامس : تحقق من ان الاقتران التالي حلا للمعادلة التفاضلية 

المعادلة التفاضلية 

المعادلة التفاضلية هي معادلة من الرتبة الاولى وغير خطية 
المشتقة الاولى للاقتران هو حاصل ضرب اقترانين ( مشتقة الاول ×الثاني + مشتقة الثاني × الاول )

مشتقة الsin هي cos 

اذن المشتقة للاقتران على الشكل التالي 

بالتعويض في المعادلة التفاضلية عن قيمة الاقتران والمشتقة 

باستخدام عملية توزيع x على عملية الجمع 

والان باخذ x^2 عامل مشترك واستخدام قوانين الاقترانات المثلثية 

بالتعويض عن sin x=y/x من الاقتران نفسه 

وبالتالي ينتج ان الطرف الايسر يساوي الطرف الايمن اذن الاقتران حلا للمعادلة التفاضلية